视频

词法分析

问题定义：
Input：程序文本/字符串(CharStream) + 词法单元(token)的规约
Output: 词法单元流(TokenStream)
我们要实现一个词法分析器解决上述问题。
词法单元的规约：即告诉我们词法是什么样子，什么格式会被划分为一个词法单元。

词法分析器的三种设计方法(由易到难)：利用词法分析器生成器、手写词法分析器、自动化词法分析器(手写)

利用词法分析器生成器，以ANTLR4为例
输入：词法单元的规约：文件名.g4
输出：文件名Lexer.java(以java为例)

接下来我们将我们想要编译的.c文件交给已经编译好的生成的.java文件，即我们的词法分析器，就能输出我们需要的词法单元流

ANTLR4使用

自动化词法分析器

.g4文件的描述语言其实就是正则表达式
(Regular Expression)

而手写词法分析器，实际上是在用代码去模拟状态转移图——术语为自动机

DFA：确定性有穷自动机
通过模拟DFA的运行，就可以较容易且机械地得到我们的词法分析器

那么我们要做的，就是将正则表达式转化到自动机。问题就是什么是正则表达式，什么是自动机，该如何将正则表达式转化到自动机。

直接将正则表达式转移到DFA是不容易的，而将正则表达式转化到NFA（非确定性有穷自动机）是容易的，将NFA转化到DFA也是相较容易的。所以我们将RE->NFA->DFA

正则表达式

Definition:
给定字母表 $\Sigma$ , $\Sigma$ 上的正则表达式由且仅由以下规则定义：
(1) $\epsilon$ 是正则表达式（空串是正则表达式）
(2) $\forall a\in \Sigma$ , $a$ 是正则表达式
(3) 如果 $r$ 是正则表达式，则( $r$ )是正则表达式
(4) 如果 $r$ 与 $s$ 是正则表达式，则 $r|s, rs, r^*$ 也是正则表达式
运算优先级：()>*>连接>|

自动机理论

有穷自动机是一类极其简单的计算装置，它可以识别（接受/拒绝） $\Sigma$ 上的字符串

非确定性有穷自动机（NFA, Nondeteministic Finite Automaton）

Definition:
非确定性有穷自动机 $A$ 是一个五元组 $A=(\Sigma, S, s_0, \delta, F)$ :
(1) 字母表 $\Sigma (\epsilon\notin\Sigma)$
(2) 有穷的状态集合 $S$
(3) 唯一的初始状态 $s_0\in S$ （此处唯一可有可无，即初始状态不唯一的NFA可以等价转换为初始状态唯一的NFA）
(4) 状态转移函数 $\delta$ :

$\delta:S\times(\Sigma\cup \{\epsilon\}) \rightarrow 2^S$

(5) 接受状态集合 $F\subseteq S$

Q：为什么叫做非确定性的有穷自动机？或者说非确定性从哪体现
A：主要看 $\delta$ 函数，即在一个字符的驱动下可以跑到不同的状态上去，这个状态是不确定的；同时也可以不需要任何字符的驱动(通过 $\epsilon$ )，自发的跑到某个状态上去
约定：所有没有对应出边的字符默认指向空状态/死状态 $\phi$

确定性有穷自动机（DFA, Deteministic Finite Automaton）

Definition:
确定性有穷自动机 $A$ 是一个五元组 $A=(\Sigma, S, s_0, \delta, F)$ :
(1) 字母表 $\Sigma (\epsilon\notin\Sigma)$
(2) 有穷的状态集合 $S$
(3) 唯一的初始状态 $s_0\in S$
(4) 状态转移函数 $\delta$ :

$\delta:S\times\Sigma\rightarrow S$

(5) 接受状态集合 $F\subseteq S$

约定：所有没有对应出边的字符默认指向一个死状态

接受/识别

Definition:
有穷自动机 $A$ 接受字符串 $x$ ，当且仅当存在一条从开始状态 $s_0$ 到某个接受状态 $f\in F$ ，标号为 $x$ 的路径

由此， $A$ 定义了一种语言 $L(A)$ :它能接受的所有字符串构成的集合

则关于自动机 $A$ ,就有两个基本问题：
(1) Membership问题：给定字符串 $x$ ， $x\in L(A)$ 吗？
(2) $L(A)$ 究竟是什么（即 $L(A)$ 对应的正则表达式）？

想要实现自动化的词法分析器，我们要有如下过程：
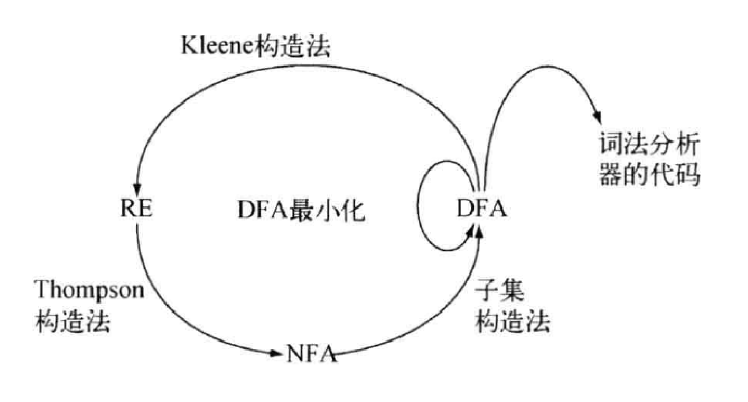
lexer1
为什么要引入NFA，因为从RE到NFA容易找到对应的 $L(A)$ ，而通过DFA容易得到词法分析器

Thompson构造法

因为无论是谁构造的正则表达式RE，都遵循RE的定义（四个条件）。则我们需要找到一个方法，按其定义中的规则能构造出相应的NFA即可。那么不管给定哪个RE，只要通过该规则就可以逐步归纳构造出最终的NFA。
规则：
(1) $\epsilon$ 是正则表达式（空串是正则表达式）
一个初态，一个终态，只接受一个 $\epsilon$ 转移到终态
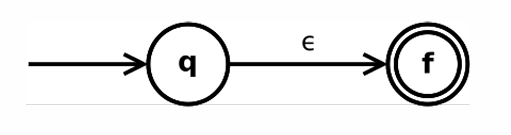
lexer2
(2) $\forall a\in \Sigma$ , $a$ 是正则表达式
一个初态，一个终态，只接受一个 $a$ 转移到终态
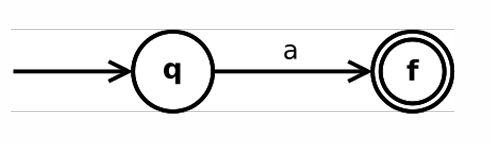
lexer3
(3) 如果 $r$ 是正则表达式，则( $r$ )是正则表达式
归纳的过程，即®对应的NFA和r对应的NFA是一样的
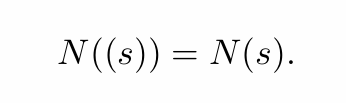
lexer4
(4) 如果 $r$ 与 $s$ 是正则表达式，则 $r|s, rs, r^*$ 也是正则表达式

$r|s:$
简称2+4
2：一个最终结果的初态，一个最终结果的终态
4：4条通过 $\epsilon$ 转移状态的边，分别为：最终结果的初态指向 $r$ 的初态， $r$ 的终态指向最终结果的终态，最终结果的初态指向 $s$ 的初态， $s$ 的终态指向最终结果的终态
$rs:$
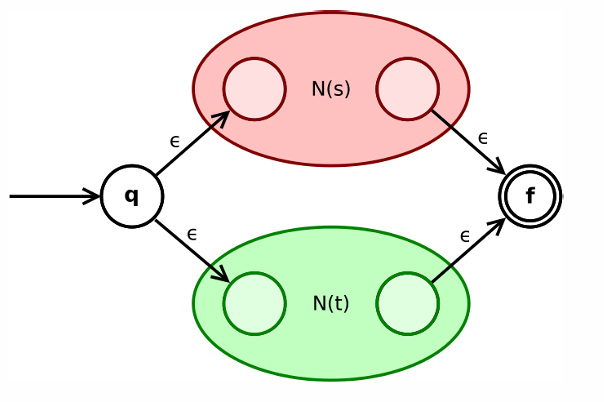
即最终结果的初态为 $r$ 的初态，最终结果的终态为 $s$ 的终态，而 $r$ 的终态和 $s$ 的初态合并
$r^*:$
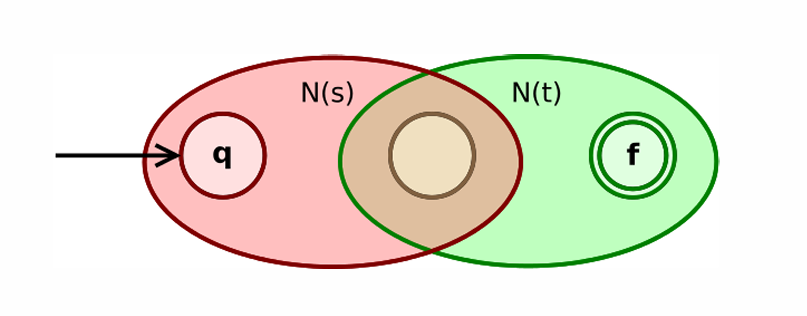
简称转一转和2+4
2：一个最终结果的初态，一个最终结果的终态
4：4条通过 $\epsilon$ 转移状态的边，分别为：最终结果的初态指向 $r$ 的初态，最终结果的初态指向最终结果的终态， $r$ 的终态指向最终结果的终态， $r$ 的终态指向 $r$ 的初态
转一转：即通过 $\epsilon$ ，从 $r$ 的终态转移到 $r$ 的初态这一情况的描述

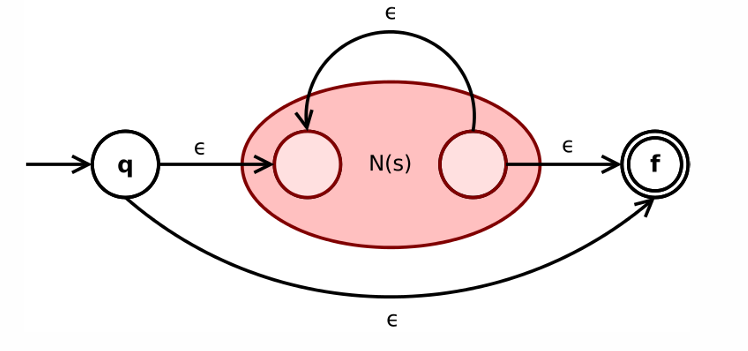
注意，根据归纳假设，过程中N(s)和N(t)的开始状态(初态)和接受状态(终态)皆唯一。即在Thompson构造的过程中的NFA的初态终态皆是唯一的。

$N(r)$ 的性质以及Thompson构造法复杂度分析：

$N(r)$ 的开始状态与接受状态均唯一
开始状态没有入边，接受状态没有出边
$N(r)$ 的状态数 $|S|\leq 2\times|r|$ ( $|r|:r$ 中运算符与运算分量的总和，因为每一步最多添加一个初态和一个终态)
每个状态最多有两个 $\epsilon$ -入边和两个 $\epsilon$ -出边
$\forall a\in\Sigma$ ，每个状态最多有一个 $a$ -入边与一个 $a$ -出边

子集构造法

实现从NFA向DFA的转化，即满足 $L(D)=L(N)$
思想是通过DFA来模拟NFA，即让构造得到的DFA的每个状态对应于NFA的一个状态集合
过程：由于无法一下子确定DFA的所有状态，只有它的初始状态可以确定。所以我们从初始状态出发，在一个字符的驱动下对其进行扩展，直到无法扩展为止。同时由于 $\epsilon$ 的存在，可以使扩展过程继续。综上所述，我们先确定初态的 $\epsilon$ -闭包，再通过一个字符的驱动下进行扩展，计算扩展集合的 $\epsilon$ -闭包，直至无法扩展为止。最终结果的DFA，其初态即最开始的初态，而终态则为对应的NFA状态集合中是否存在NFA中的终态。

形式化如下:
$\epsilon$ -闭包：从状态s开始，只通过 $\epsilon$ -转移可达的状态集合：

$\epsilon-closure(s)=\{t\in S_N|s\mathop{\rightarrow}\limits^{\epsilon^*}t\}$

$\epsilon-closure(T)=\mathop{\bigcup}\limits_{s\in T}\epsilon-closure(s)$

$move(T,a)=\mathop{\bigcup}\limits_{s\in T}\delta(s,a)$

则子集构造法原理：

$N:(\Sigma_N,S_N,n_0,\delta_N,F_N)$

$D:(\Sigma_D,S_D,d_0,\delta_D,F_D)$

字母表相同

$\Sigma_D=\Sigma_N$

即DFA中的任意一个状态，都对应NFA中的一个状态集合（表示为NFA状态集S_N的子集）

$S_D\subseteq 2^{S_N}(\forall s_D\in S_D:s_D\subseteq S_N)$

初始状态 $d_0=\epsilon-closure(n_0)$
即对DFA中的任意一个状态作 $a$ -转移后还要作 $\epsilon$ -闭包
转移函数 $\forall a\in\Sigma_D:\delta_D(s_D,a)=\epsilon-closure(move(s_D,a))$
接受状态集 $F_D=\{s_D\in S_D|\exists f\in F_N, f\in s_D\}$

子集构造法的复杂度分析：
$|S_N|=n$ ， $|S_D|=\Theta(2^n)=O(2^n)\cap\Omega(2^n)$
对于任何算法(包括子集构造法)，最坏情况下， $|S_D|=\Omega(2^n)$
因为NFA转化到DFA，DFA的每一个状态对应NFA的一个状态集合，其实就是对应NFA状态集的子集，又因为 $|S_N|=n$ ，所以NFA状态集的子集个数就是 $2^n$ ，那么DFA的状态数最多也不会超过 $2^n$ 。但可惜的是子集构造法的下界也是 $2^n$ 的复杂度。

闭包的概念可以这么理解：如求某个闭包 $f-closure(T)$ ，T为状态集合
$T\Rightarrow f(T)\Rightarrow f(f(T))\Rightarrow f(f(f(T)))\Rightarrow ...$
直到找到一个 $x$ 使得 $f(x)=x$ ， $x$ 称为 $f$ 的不动点。

DFA最小化

基本思想：等价的状态可以合并
这里等价的定义并不是对字母表的任意字母，s和t都能到达同一个状态，就说明s和t等价，即下述形式化错误

$s\sim t\iff \forall a\in\Sigma. \big(((s\mathop{\rightarrow}\limits^as')\land(t\mathop{\rightarrow}\limits^at'))\big)\Rightarrow (s'=t')$

正确表示形式化如下：

$s\sim t\iff \forall a\in\Sigma. \big(((s\mathop{\rightarrow}\limits^as')\land(t\mathop{\rightarrow}\limits^at'))\big)\Rightarrow (s'\sim t')$

即通过一个字符，能走到等价的状态上。
那么s和t不等价的形式化表述如下：

$s≁ t\iff \forall a\in\Sigma. (s\mathop{\rightarrow}\limits^as')\land(t\mathop{\rightarrow}\limits^at')\land(s'≁ t')$

Definition（可区分的；等价的）：
如果存在某个能区分状态 $s$ 与 $t$ 的字符串，则称 $s$ 与 $t$ 是可区分的；否则，称 $s$ 与 $t$ 是等价的。
Definition（字符串 $x$ 区分状态s与t）：
如果分别从 $s$ 和 $t$ 出发，沿着标号为 $x$ 的路径到达的两个状态只有一个是接受状态，则称 $x$ 区分了状态s与t。

那么一个基本的想法就是基于该定义，不断合并等价的状态，直到无法合并为止。但我们知道，这是一个递归定义，我们该从哪里开始呢？如果我们根据该定义，就要不断地向前寻找状态是否等价，而我们是找不到这么一个递归的基础/起点的。因为我们开始并不能根据定义判断状态是否等价
所以我们改变我们的想法，从合并改为划分，即从将等价的状态合并在一起改为针对某个状态集合，将不等价的给划分开来。并且开始，我们就可以将接受状态和非接受状态划分开来，他们必然不等价。
具体DFA最小化过程方法如下：
$\Pi=\{F,S \setminus F \}$
令 $\Pi_{new}=\Pi$
遍历 $\Pi$ 中的每个划分 $G$ ，尝试将 $G$ 划分为更小的组。 $G$ 中的状态 $s$ 和 $t$ 在同一小组，当且仅当对 $\forall a\in\Sigma$ ,状态 $s$ 和 $t$ 在 $a$ 上的转化都到达在 $\Pi$ 中的同一组。
然后对 $\Pi_{new}$ 作更新。上述遍历和更新过程直至无法再划分为止，然后将同一等价类的状态合并（即在同一划分里的状态）
Q：状态合并后是否还是DFA
A：显然还是DFA，合并后若能达到不同状态说明之前的划分过程还未结束
Q：合并后开始状态和接受状态如何确定
A：即原DFA的开始状态和接受状态在哪个划分里，该划分合并后为开始/接受状态

如何分析DFA最小化算法的复杂度？为什么DFA最小化算法是正确的？最小化DFA是唯一的吗？
DFA Minimization @ wiki

词法分析器遵循最前优先匹配，最长优先匹配
词法分析时NFA转化为DFA时，需要消除死状态。

一个简单的语法制导翻译器

2.1 引言

编译器在分析阶段把一个源程序划分成各个组成部分，并生成源程序的内部表达形式。这种内部表示称为中间代码。然后，编译器在合成阶段将这个中间代码翻译成目标程序。
分析阶段的工作围绕着编译语言的“语法”展开。一个程序设计语言的语法描述了该语言的程序的正确形式，而该语言的语义则定义了程序的含义，即每个程序在运行时做什么事情。2.2节中，我们将通过上下文无关文法或**BNF(Backus-Naur范式)**来描述语法。结合非形式化描述和启发性的示例来描述语义。上下文无关文法不仅可以描述一个语言的语法，还可以指导程序的翻译过程。在2.3节中，我们将介绍一种面向文法的编译技术，即语法制导翻译技术。2.4节中将介绍语法扫描/语法分析。其余部分将快速浏览下图中的编译器前端模型。
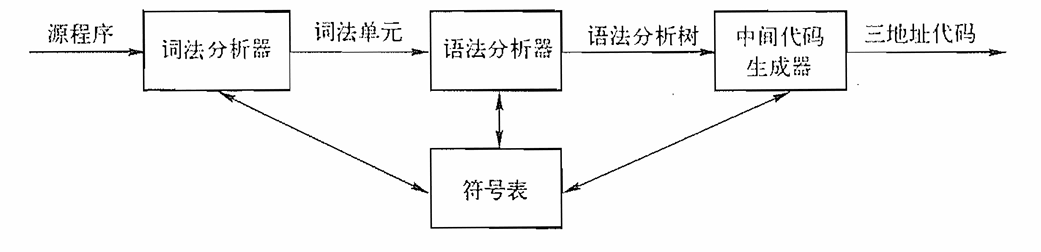
forward
首先将介绍语法分析器。比如考虑从中缀表达式翻译到后缀表达式。词法分析器使得翻译器可以处理由多个字符组成的构造，比如标识符。标识符由多个字符组成，但在语法分析阶段被当作一个词法单元(token)处理。接下来将考虑中间代码的生成，由两种中间代码形式，一种是抽象语法树AST(Abstract Syntax Tree)，简称为语法树；另一种是三地址代码

2.2 语法定义

本节中，介绍一种用于描述程序设计语言语法的表示方法——“上下文无关文法”，简称“文法”。在本书中，文法将被用于组织编译器前端。
文法自然地描述了大多数程序化设计语言构造的层次化语法结构。例如，Java中的if-else语句通常具有如下形式

$\textbf{if}\ (expression)\ statement\ \textbf{else}\ statement$

即一个if-else语句由关键字if、左括号、表达式、右括号、一个语句、关键字else和另一个语句连接而成。如果我们用变量expr来表示表达式，用变量stmt表示语句，那么构造规则可以表示为

$stmt\rightarrow\ \textbf{if}\ (expr)\ stmt\ \textbf{else}\ stmt$

其中箭头可以读作“可以具有如下形式”。这样的规则称为产生式。在一个产生式中，像关键字if和括号这样的词法元素称为终结符号。像expr和stmt这样表示终结符号序列的变量，它们称为非终结符号。

2.2.1 文法定义

一个上下文无关文法(context-free grammar) $G$ 由四个元素组成 $G=(V_N,V_T,P,Z)$ ：
(1) $V_N$ ：非终结符号集。它们有时也称为“语法变量”。每个非终结符号表示一个终结符号串的集合。
(2) $V_T$ ：终结符号集。它们有时也称为“词法单元”。终结符号是该文法所定义的语言的基本符号的集合。即对应词法分析器产生的词法单元
(3) $P$ ：产生式或规则的集合。其中每个产生式包括一个称为产生式头或左部的非终结符号，一个箭头，和一个称为产生式体或右部的由终结符号及非终结符号组成的序列。产生式主要用来表示某个构造的某种书写形式。如果产生式头非终结符号代表一个构造，那么该产生式体就代表了该构造的一种书写方式。
(4) $Z$ ：开始符号（识别符号） $Z\in V_N$ 。指定一个非终结符号为开始符号。
在描述文法的时候，我们会列出该文法的产生式，并且首先列出开始符号对应的产生式。在本书中我们假设数位、符号（如 $<,\leq$ ）和黑体字符串都是终结符号。斜体字符串表示非终结符号，所有非斜体的名字或符号都可以看作是终结符号。为表示方便，以同一个非终结符号为头部的多个产生式的体可以放在一起表示，不同体之间用符号|分隔。
例2.1：比如有多个使用数位和+、-符号组成的表达式，如9-5+2、3-1或7.我们把这样的表达式称为“由+、-号分隔的数位序列”。下面的文法描述了这种表达式的语法。此文法的产生式包括：

$list\rightarrow list + digit$

$list\rightarrow list - digit$

$list\rightarrow digit$

$digit\rightarrow 0\ |1\ |2\ |3\ |4\ |5\ |6\ |7\ |8\ |9$

以非终结符号 $list$ 为头部的三个产生式可以等价地组合为：

$list\rightarrow list+digit|list-digit|digit$

根据习惯，该文法终结符号为

$+\ -\ 0\ 1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9$

该文法的非终结符号是 $list$ 和 $digit$ 。因为 $list$ 的产生式首先被列出，所以我们知道 $list$ 是此文法的开始符号。
如果某个非终结符号是某个产生式的头部，我们就说该产生式是该非终结符号的产生式。一个终结符号串是由零个或多个终结符号组成的序列。零个终结符号组成的串称为空串，记为 $\epsilon$

2.2.2 推导

根据文法推导符号串时，我们首先从开始符号出发，不断将某个非终结符号替换为该非终结符号的某个产生式的体。可以从开始符号推导得到的所有终结符号串的集合称为该文法定义的语言
法。如果不能从文法的开始符号推导得到该终结符号串，则报告该终结符号串中包含的语法错误。
推导即是将某个产生式的左部替换成它的右部，关键在于每一步推导要替换哪个非终结符合，以及使用哪个产生式。
而语法分析的任务是：接受一个终结符号串作为输入，找出从文法的开始符号推导出这个串的方法。如果不能从文法的开始符号推导得到该终结符号串，则报告该终结符号串中包含的语法错误。

2.2.3 语法分析树

语法分析树用图形方式展现了从文法的开始符号推导出相应语言中的符号串的过程。如果非终结符号A有一个产生式 $A\rightarrow XYZ$ ，那么在语法分析树中就可能有一个标号为A的内部结点，该结点有三个子结点，从左向右标号分别为X、Y、Z：
tree
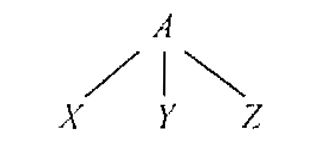
正式地讲，给定一个上下文无关文法，该文法的一棵语法分析树(parse tree)是具有以下性质的树：
(1) 根结点的标号为文法的开始符号
(2) 每个叶子结点的标号为一个终结符号或 $\epsilon$
(3) 每个内部结点的标号为一个非终结符号
(4) 如果非终结符号 $A$ 是某个内部结点的标号，并且它的子结点的标号从左至右分别为 $X_1,X_2,...,X_n$ ，那么必然存在产生式 $A\rightarrow X_1X_2...X_n$ ，其中 $X_1,X_2,...,X_n$ 既可以是终结符号，也可以是非终结符号。作为一个特殊情况，如果 $A\rightarrow\epsilon$ 是一个产生式，那么一个标号为A的结点可以只有一个标号为 $\epsilon$ 的子结点。
一棵语法分析树的叶子结点从左向右构成了树的结果，也就是从这棵语法分析树的根结点上的非终结符号推导得到的符号串。
一个文法的语言的另一个定义是指任何能够由某棵语法分析树生成的符号串的集合。为一个给定的终结符号串构建一棵语法分析树的过程称为对该符号串进行语法分析。

2.2.4 二义性

一个文法可能有多棵语法分析树能够生成同一个给定的终结符号串。这样的文法称为具有二义性。要证明一个文法具有二义性，我们只需要找到一个终结符号串，说明它是两棵以上语法分析树的结果。由于具有两棵以上语法分析树的符号串通常具有多个含义，所以我们需要为编译应用设计出没有二义性的文法，或者在使用二义性文法时使用附加的规则来消除二义性。
比如将之前
例2.5：假如将例2.1中的文法改写如下

$string\rightarrow string+string|string-string|0\ |1\ |2\ |3\ |4\ |5\ |6\ |7\ |8\ |9$

即将 $digit$ 和 $list$ 合并为非终结符号 $string$ 是有一些意义的，因为单个 $digit$ 是 $list$ 的一个特例。但这种做法会导致像9-5+2这样的表达式有多棵语法分析树，导致对应两种带括号的表达式:(9-5)+2和9-(5+2)。而这会导致不同的结果。
若文法是二义性的，则在编译时就会产生不确定性，遗憾的是在理论上已经证明文法的二义性是不可判定的。

2.2.5 运算符的结合性

当一个运算分量的左右两侧都有运算符时，我们需要一些规则来决定哪个运算符被应用于该运算分量。我们说运算符“+”是左结合的，因为当一个运算分量左右两侧都有“+”号时，它属于其左边的运算符。在大多数程序设计语言中，加减乘除四种算术运算符都是左结合的。某些常用运算符是右结合的，比如指数运算或者C语言中的赋值运算符。

2.2.6 运算符的优先级

结合性规则只能作用于同一运算符的多次出现，因此当多种运算符出现时，我们需要给出一些规则来定义运算符之间的相对优先关系。
一般对于n层优先级的情况。我们需要n+1个非终结符号。用n个非终结符号对应n层优先级，再用额外的一个的产生式体为单个运算分量或括号括起来的表达式。然后对于每个优先级都有一个非终结符，表示能被该优先级或更高优先级的运算符分开的表达式。

Definition：
句型：如果 $S\mathop{\Rightarrow}\limits^{*}\alpha$ ，且 $\alpha\in(V_T\cup V_N)^{*}$ ，则称 $\alpha$ 是文法 $G$ 的一个句型
Definition:
句子：如果 $S\mathop{\Rightarrow}\limits^{*}w$ ，且 $w\in V_T^{*}$ ，则称 $w$ 是文法G的一个句子。
Definition：
文法 $G$ 的语言 $L(G)$ ：是它能推导出的所有句子构成的集合。

$L(G)=\{w|S\mathop{\Rightarrow}\limits^{*}w,w\in V_T^*\}$

同样关于文法也有两个基本问题：
(1) Membership问题：给定字符串 $x\in V_T^*$ ， $x\in L(G)$ 吗？
(2) $L(G)$ 究竟是什么？

第一个问题对应的就是语法分析器的任务：为输入的词法单元流寻找推导、构建语法分析树，或者报错
而第二个问题是程序设计语言设计者需要考虑的问题

接下来我们证明正则表达式的表达能力严格弱于上下文无关文法
我们的思路可以先是证明正则表达式的表达能力不强于上下文无关文法，即正则表达式所表达的语言都可以用上下文无关文法来表示。在此基础上证明严格弱于的话，只需要找到一个语言，它可以用上下文无关文法来表示，却不能用正则表达式来表示即可。

每个正则表达式 $r$ 对应的语言 $L(r)$ 都可以使用上下文无关文法来描述
证：先将 $r$ 转化为相应的NFA，然后根据NFA的转移函数 $\delta$ ,即若 $\delta(A_i,a)=A_j,a\in\Sigma$ ，则对应一条产生式 $A_i\rightarrow aA_j$ ，另外若有 $\delta(A_i,\epsilon)=A_j$ ，则有产生式 $A_i\rightarrow A_j$ ,而上下文无关文法所需的终结符号集合和非终结符号集合和开始符号相应按定义构造得到即可。
下证正则表达式的表达能力严格弱于上下文无关文法的表达能力：
证明 $L=\{a^nb^n|n\geq0\}$ 无法使用正则表达式描述。采用反证法。假设存在正则表达式 $r$ ，其 $L(r)=L$ 。那么则存在一个有限状态自动机 $D(r)$ ，使得 $L(D(r))=L$ ，设其状态数为 $k\geq1$ 。接下来我们考虑输入为 $a^m(m\geq k)$ 的情况
首先状态机每读入输入的一个字符，会发生状态的转移。对于 $a^m$ ，包括开始状态，总共要经历 $m+1$ 个状态，而状态机总共只有 $k(m\geq k)$ 个状态，那么根据鸽巢原理，对于 $a^m$ 至少会经历两个相同的状态，可以绘图如下

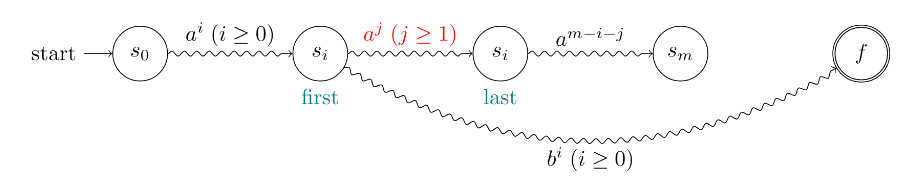
记这个重复出现的状态为 $s_i$ ,以 $s_i$ 作为一头一尾将状态机划分为上述部分。那么对于字符串 $a_ib_i$ ，这个状态机理应接受，转移如上图所示。那么对于字符串 $a_{i+j}b_i$ ，这个状态机理应也能接受，但这与 $L(D(r))$ 不符，产生矛盾，得证。

Pumping Lemma：
即对一个正则语言 $L$ ，会存在一个数 $p\geq1$ (pumping length)，使得该语言中所有长度大于等于 $p$ 的字符串 $s$ 可以被分为三个部分，即 $s=xyz$ ，同时满足下述条件：

$|y|\geq 1$
$|xy|\leq p$
$\forall i\geq0:xy^iz\in L$
通常用来判断一个语言是否是正则语言，通常利用第三条导出矛盾

语法分析

递归下降的LL(1)语法分析器

自顶向下构建语法分析树，只考虑无二义性的文法。
即最后目的是构建自顶向下的、递归下降的、基于预测分析表的、适用于 $LL(1)$ 文法的 $LL(1)$ 语法分析器

自顶向下

从根节点开始构建语法分析树。根节点是文法的起始符号 $S$ ，叶节点是词法单元流 $w$ $，仅包含终结符号与特殊的文件结束符$(EOF，我的老师应该采用了#表示)。每个中间节点表示对某个非终结符应用某个产生式进行推导（关键在于选择哪个非终结符，以及选择哪个产生式）
在推导的每一步， $LL(1)$ 总是选择最左边的非终结符进行展开。 $LL(1)$ 的第一个 $L$ 表示的是从左向右读入词法单元，第二个 $L$ 表示选择最左边的非终结符进行展开。

递归下降

即实现语法分析器时，为每个非终结符写一个递归函数，内部按需调用其他非终结符对应的递归函数，下降一层(也可采用迭代)

Definition：
如果文法 $G$ 的预测分析表是无冲突的，则 $G$ 是 $LL(1)$ 文法。
无冲突指的是对于当前选择的非终结符，仅根据输入中当前的词法单元即可确定需要使用哪条产生式。

预测分析表的构建

FIRST集

Definition(FIRST( ${\alpha}$ )集合)：
对于任意的 $\alpha\in(V_N\cup V_T)^*$ :

$FIRST(\alpha)=\{t\in V_T\cup \{\epsilon\}|\alpha\mathop{\Rightarrow}\limits^* t\beta\vee\alpha\mathop{\Rightarrow}\limits^*\epsilon\}$

即 $FIRST(\alpha)$ 是可从 $\alpha$ 推导得到的句型的首终结符号的集合
一般求产生式右部的 $FIRST(\alpha)$ ，这样在当前的非终结符时，根据当前的词法单元就可以根据 $FIRST(\alpha)$ 选择相应的产生式
Definition(FOLLOW( $A$ )集合)
对于任意的非终结符 $A\in V_N$ :

$FOLLOW(A)=\{t\in V_T\cup \{\$\}|\exist s. S\mathop{\Rightarrow}\limits^* s\triangleq\beta At\gamma\}$

即 $FOLLOW(A)$ 是可能在某些句型中紧跟在A右边的终结符的集合。作用是，考虑产生式 $A\rightarrow\alpha$ ，如果从 $\alpha$ 可能推导出空串，即 $\alpha\mathop{\Rightarrow}\limits^*\epsilon$ ，则持有当前词法单元 $t$ 时，只有当 $t\in FOLLOW(A)$ 时，才能选择该产生式

计算FIRST集合

上图对应计算的为每个符号 $X\in V_N\cup V_T$
有了单个符号的 $FIRST$ 集合，那么对于符号串 $\alpha$ ， $FIRST(\alpha)$ 如下：

$\alpha=X\beta\\ FIRST(\alpha)= \begin{cases} FIRST(X)& X\mathop{\not\Rightarrow}\limits^*\epsilon 或\epsilon\not\in L(X)\\ (FIRST(X)\setminus{\epsilon})\cup FIRST(\beta)& X\mathop{\Rightarrow}\limits^*\epsilon或\epsilon\in L(X) \end{cases}$

或的后面是视频中的形式，前面是我认为更容易理解的形式，但应是等价的。

计算FOLLOW集合

首先注意 $FOLLOW$ 集合针对的是非终结符号。对开始符号的 $FOLLOW$ 集增加文件结束符$，是因为本身匹配的词法单元流形式为 $w\$$ ，而推导又都是从开始符号开始，并且我们希望开始符号与 $w$ 能够匹配。所以$要被放到开始符号的 $FOLLOW$ 集合里
然后对于规则2，即证该条件下 $FOLLOW(A)\subseteq FOLLOW(X)$ ，即要说明 $\forall t\in FOLLOW(A),t\in FOLLOW(X)$
证明如下,记开始符号为S:

$t\in FOLLOW(A)\rightarrow S\mathop{\Rightarrow}\limits^*...At...\\ A\rightarrow\alpha X,S\mathop{\Rightarrow}\limits^*...\alpha Xt,则根据定义,t\in FOLLOW(X)$

而对于规则3，注意 $\epsilon\in FIRST(\beta)$ 的情况

SELECT集合

我的课内PPT还定义了SELECT集合如下：
对于给定产生式 $A\rightarrow\alpha, A\in V_N, \alpha\in V^*$ ，则

$SELECT(A\rightarrow\alpha)= \begin{cases} FIRST(\alpha)& if& \alpha\mathop{\not\Rightarrow}\limits^*\epsilon\\ FIRST(\alpha)\cup FOLLOW(A)& else \end{cases}$

这可能是为了便于理解引入的中间概念，但其实可以直接利用 $FIRST和FOLLOW$ 去填写预测分析表

预测分析表

对于给定文法 $G$ ，对应每条产生式 $A\rightarrow\alpha$ 与终结符 $t$ ，如果满足以下任意一个条件

$\begin{align} & t\in FIRST(\alpha) \\ & \alpha\mathop{\Rightarrow}\limits^*\epsilon\land t\in FOLLOW(A) \end{align}$

那么则在表格 $[A,t]$ 填入 $A\rightarrow\alpha$

总结 $LL(1)$ 语法分析器：
$first-L$ : 从左向右扫描输入
$second-L$ : 构建最左推导
$1$ : 只需向前看一个输入符号便可确定使用哪条产生式

LL(1)文法

自顶向下的分析方法需要文法必须是LL(1)的形式。